– Representasjoner er nødvendige for å uttrykke matematiske ideer, sier Bjørnar Alseth. Han er en av forfatterne av matematikkverket Multi og har forsket på barns læring i matematikk. – De kan brukes til å løse oppgaver og problemer, og for å tenke og kommunisere om matematiske ideer.

Bjørnar trekker fram denne oppgaven som et eksempel: «Emil har fem grankongler og tre furukongler. Hvor mange kongler har han til sammen?» For å svare på oppgaven kan eleven telle og løfte opp fem fingre på den ene hånden og tre på den andre. Da kan eleven telle alle fingrene som er løftet og dermed blir fingrene en konkret representasjon. Elevene kan også bruke objekter eller tegninger:

– Har man tilgang på både furu- og grantrær kan elevene selv sanke kongler og telle dem, men en enklere løsning er kanskje å tegne fem grankongler og tre furukongler, og deretter telle hvor mange det er til sammen, sier Bjørnar.
Fra konkret til abstrakt
En mer abstrakt representasjonsformen er å bruke ikoner. Eleven kan for eksempel tegne fem streker for grankonglene og tre sirkler for furukonglene.
– Det er mer effektivt enn å bruke lang tid på å tegne fine kongler, men til gjengjeld er det ikke lenger enkelt å forstå at tegningen dreier seg om kongler, fortsetter Bjørnar.
Den mest abstrakte representasjonsformer er å bruke symboler. Da kan eleven representere tekstoppgaven som 5 + 3.
– Fordelen med abstrakte representasjonsformer er at de er veldig effektive. De er godt egnet til å representere matematiske ideer, men de er i utgangspunktet vanskelige å forstå. Tegninger og konkreter er enklere å forstå, men er mer tidkrevende og omstendelige for eleven.

Tallene er toppen av isfjellet
Men hvorfor bør vi gå den litt tidkrevende omveien med kongler og fingre og streker når vi skal lære og forstå matematiske problemstillinger?
– Hvis en elev strever med matematikk kan en av flere grunner være for tidlig abstraksjon av matematiske ideer, sier Mona Røsseland. Hun er førsteamanuensis ved Høgskulen på Vestlandet og en av Multi-forfatterne.
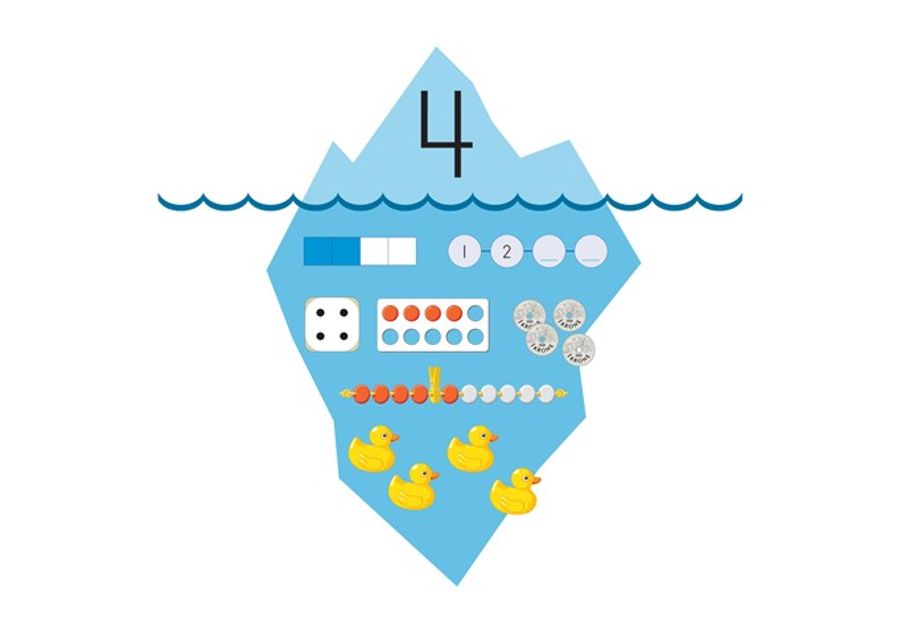
– Ved å bruke mange ulike representasjonsformer og se disse i sammenheng, viser forskning at forståelsen kan øke. Noen forskere fremstiller dette som et isfjell. Toppen av isfjellet er tallene. Under ligger forskjellige uttrykksformer som symboler, tegninger, regnefortellinger, konkreter, diagrammer og tabeller. Man bruker ikke alle disse samtidig, men de danner grunnlaget for en mer abstrakt forståelse, forklarer Mona.
La elevene bestemme selv
I Multi vil du finne mange ulike representasjoner. På småtrinnet innledes ofte et emne med konkreter eller tegninger, men også gjennom hele mellomtrinnet brukes konkreter, bilder og diagrammer. Deretter introduseres gradvis stadig mer abstrakte representasjonsformer og symboler.
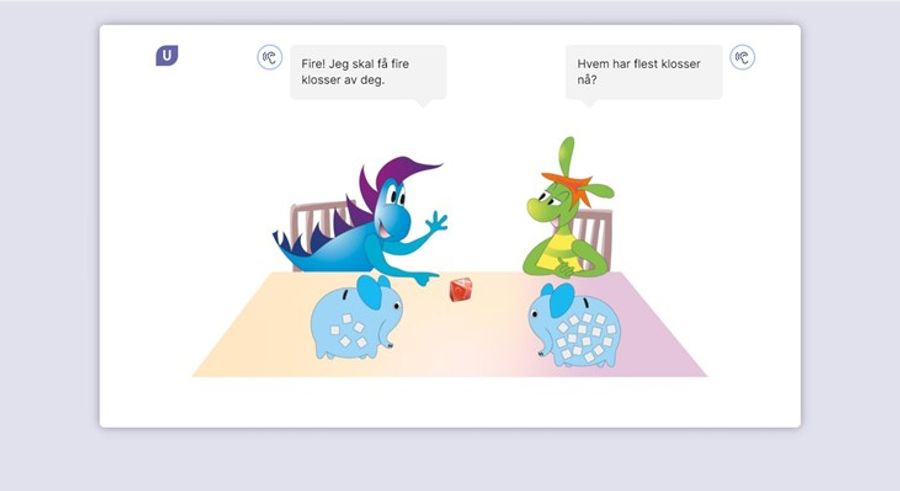
– Vi oppfordrer elevene til å velge representasjonsformer selv, både direkte i oppgaver og indirekte gjennom illustrasjoner, sier Multi-forfatter Ann-Christin Arnås. – Elevene gjør det ved å følge tips de finner i oppgaven, eller ved å utvikle egne representasjoner. Hvis elevene løser dette ulikt er det et fint utgangspunkt for samtale og diskusjon, for eksempel i en oppsummering i etterkant av en aktivitet eller utforsking. Det øker elevenes fortrolighet med ulike representasjonsformer, samtidig som elevene ser nytten av å kunne veksle mellom ulike representasjoner.
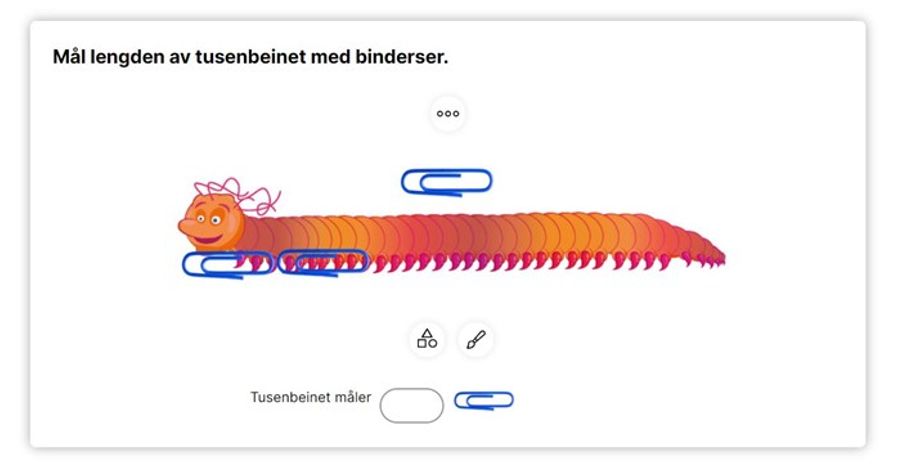
Nyttige verktøy
Jobb med representasjoner i Multi Skolestudio
I Multi Skolestudio er det utviklet en verktøykasse til hvert tema. Her vil du finne en rekke nyttige verktøy som tall-linjer, klokker, spinnere og terninger. I tillegg kan både lærer og elev utforske og bruke mange ulike konkreter i form av bilder, objekter, centicuber og base 10. Verktøyene er tilpasset temaet og trinnet, slik at du alltid vil finne det du trenger til undervisningen.
